管理運籌學就是一門解決最高效率、最大利潤、最小成本等的課程。有人說管理運籌學深不可測、高不可攀。運籌學是一門應用科學，至今還沒有統一的定義。我國出版的《管理百科全書》將運籌學定義為：“運籌學是應用分析、試驗、量化的方法，對經濟管理系統中人力、物力、財力等資源進行統籌安排，為決策者提供有依據的最優(yōu)方案，以實現最有效的管理。”運籌學作為一門綜合性多學科交叉的科學分支，未來的發(fā)展趨勢將進一步為高層次、全球性的問題提供定性與定量分析，對各種決策方案進行科學評估。運籌學的思想貫穿了企業(yè)管理的全過程，它在企業(yè)戰(zhàn)略管理、生產計劃、市場營銷、運輸問題、庫存管理、財務會計、售后服務等各個方面都具有重要的作用。運籌學為管理決策服務，使得人類在經濟發(fā)展、科學技術進步及保護環(huán)境中能更有效合理的利用有限資源。

第1講
緒論 1.1管理運籌學是什么
 1.2運籌學的決策過程
 1.3運籌學在日常管理中解決哪些問題及軟件應用
第2講
線性規(guī)劃的圖解法 2.1問題的提出
 2.2線性規(guī)劃的圖解法
 2.3圖解法靈敏度分析
第3講
線性規(guī)劃問題的計算機求解 3.1“管理運籌學”軟件介紹
 3.2手把手教你用軟件
第4講
線性規(guī)劃在工商管理中的應用 4.1人力資源如何合理分配，既能滿足工作需要又使安排人力最少
 4.2如何制定生產計劃，以獲得最大利潤
 4.3如何合理套裁下料，使原料最省
 4.4如何配置產品原料，才能獲得最大利潤
 4.5如何投資，以獲取最大收益
第5講
單純形法 5.1單純形法---知其然，知其所以然
 5.2線性規(guī)劃單純性表格求解法
 5.3如何求解成本最小的方案？
 5.4不是所有的線性規(guī)劃都有唯一最優(yōu)解
第6講
單純形法的靈敏度分析與對偶問題 6.1利潤、成本及資源變化了怎么辦？
 6.2怎么定租金？
 6.3原問題與對偶問題的關系
 6.4對偶單純形法
第7講
運輸問題 7.1如何運輸成本最小
 7.2用軟件求解
 7.3實際應用
 7.4“表上作業(yè)法”
第8講
整數規(guī)劃 8.1圖解法求解
 8.2軟件求解
 8.3實際應用
 8.4“分支定界法”簡介
 8.5 0-1規(guī)劃的解法
第9講
動態(tài)規(guī)劃 9.1單階段決策與多階段決策
 9.2最短路徑問題與多階段決策問題
 9.3動態(tài)規(guī)劃建模的有關概念
 9.4動態(tài)規(guī)劃的基本方程與最優(yōu)化原理
 9.5動態(tài)規(guī)劃的應用
第10講
存儲論 10.1不允許缺貨、生產時間很短的確定需求存儲問題
 10.2不允許缺貨、生產時間較長的確定需求存儲問題
 10.3允許缺貨、生產時間很短的確定需求存儲問題
 10.4允許缺貨、生產時間較長的確定需求存儲問題
 10.5有價格折扣的經濟訂貨批量存儲問題
 10.6報童是如何訂購報紙的
 10.7基于固定再訂貨點的隨機需求存儲問題
 10.8定期檢查庫存的隨機需求存儲問題
第11講
排隊論 11.1排隊現象背后的科學問題
 11.2只有一個服務窗口的銀行排隊系統
 11.3有多個服務窗口的銀行排隊系統，以服務窗口的最佳數量
 11.4便利店排隊系統、汽車自動沖洗排隊系統
 11.5?電話訂貨排隊系統
 11.6車間機器維修排隊系統，理發(fā)店排隊系統
第12講
對策論-博弈論初探 12.1對策論是什么
 12.2矩陣對策的最優(yōu)純策略
 12.3矩陣對策的混合策略
 12.4還有什么類型的對策論
第13講
決策分析 13.1自然狀態(tài)發(fā)生的可能性大小未知情況下如何進行決策
 13.2自然狀態(tài)發(fā)生的可能性大小已知情況下如何進行決策
 13.3為什么有的人買彩票，有的人不買彩票？

運籌學的決策過程

決策的基本原則·科學性原則：

是指決策必須尊重客觀規(guī)律，尊重科學，從實際出發(fā)，實事求是，按照科學的精神、科學的態(tài)度，運用科學的知識和方法進行決策。

·經濟性原則：

包括兩重含義：應使決策過程本身所花的費用最少；決策的內容應該堅持經濟效益標準。

·時效原則：

時效原則要求決策必須當機立斷，恰當的時機做出決策。

·群眾性原則：

決策者在進行一項決策時，必須堅持走群眾路線，應該充分依靠專家、智囊，盡量依靠大家的智慧，進行民主決策。

·滿意原則：

今天的管理學家們則認為滿意原則應當是綜合標準最優(yōu)原則，不是追求經濟效益最大的這個原則。

運籌學在日常管理中解決哪些問題及軟件應用

“管理運籌學”軟件介紹

管理運籌學軟件2.0是韓伯棠編著的《管理運籌學》的配套軟件，提供了諸如線性規(guī)劃、圖與網絡等3個方面的15個功能模塊，是學習管理運籌學的最佳工具，其中，2.0版又是之前推出的1.0版本的升級版，在界面、功能等方面均作了不小的提升和改進，同時平臺由Dos 升級為Windows。

《管理運籌學》是架構在運籌學基礎上的學科，它借助運籌學的理論方法，針對現實中的系統，特別是經濟系統進行量化分析，并以量化數據為支撐，去求得經濟系統運行的最優(yōu)化方案，以此來幫助系統運行的決策者做出科學的決策。由此可見，管理運籌學是一門以決策支持為目標的應用性學科。

本軟件主要是為學習及研究管理學、經濟學、社會學、政治學等學科服務的，本軟件的主要內容涉及的是經濟管理中的最優(yōu)規(guī)劃及決策方法等問題。通過軟件的學習和使用，可以掌握如何從定性分析向定量分析過渡，分析整理系統的有關信息去建立相應的定量分析模型，同時掌握有關的求解定量模型的數學方法。

手把手教你用軟件

1.軟件使用演示：（演示例1）第一步：點擊“開始”->“程序”->“管理運籌學

2.0”，彈出主窗口。

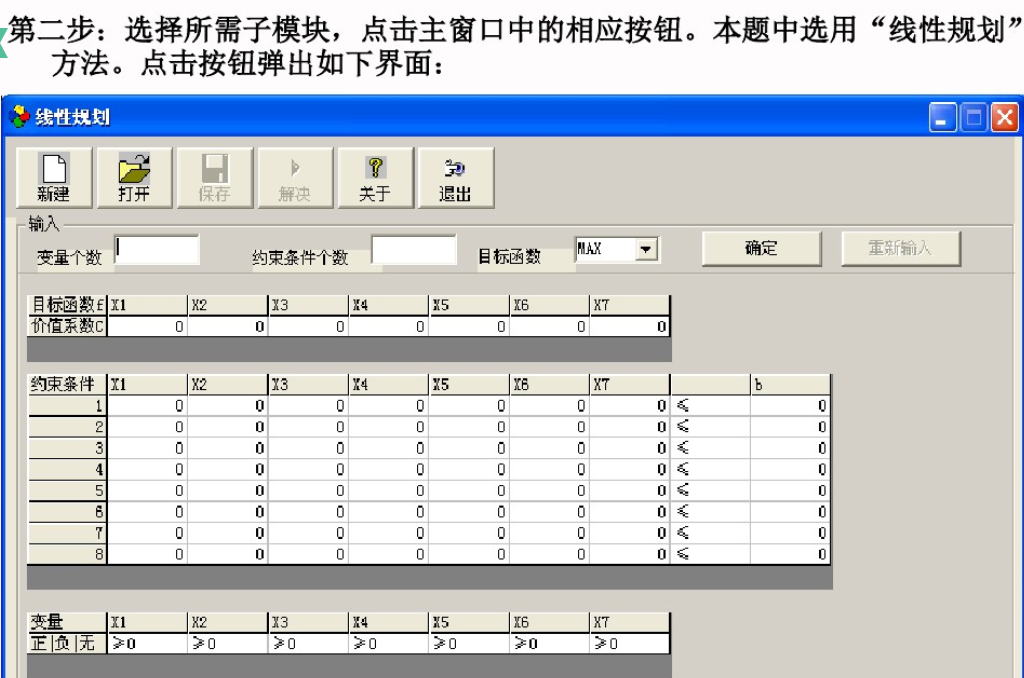
第二步：選擇所需子模塊，點擊主窗口中的相應按鈕。本題中選用“線性規(guī)劃”

方法。點擊按鈕彈出如下界面：

第三步：點擊“新建”按鈕，輸入數據。本題中共有2個變量，3個約束條件，目標函數取MAX。點擊“確定”后，在表中輸入C，b；和a等值，并確定變量的正負約束。輸入數值后的界面如下。

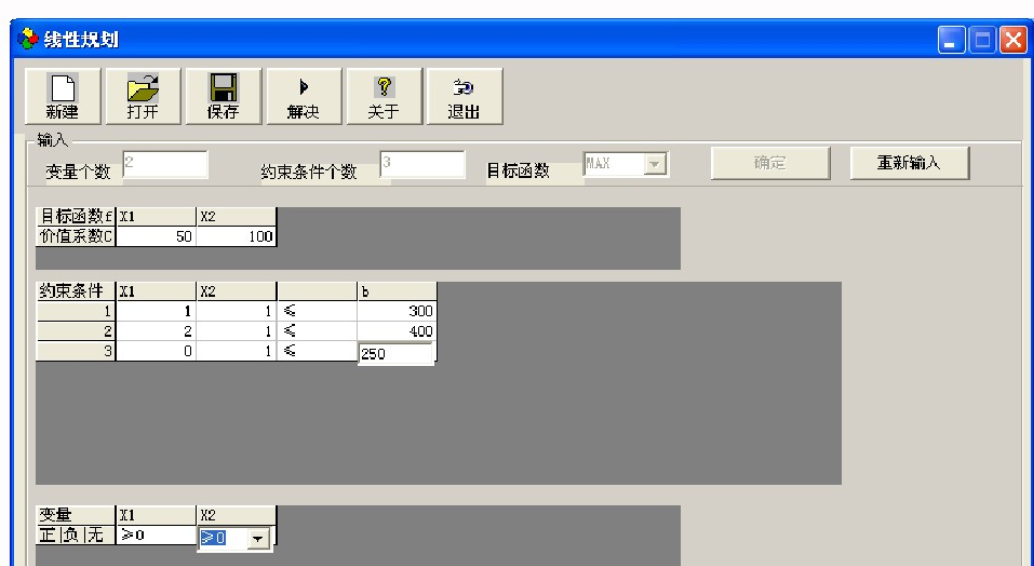
第四步：點擊“解決”按鈕，得出計算結果。本題的運行結果界面如下。

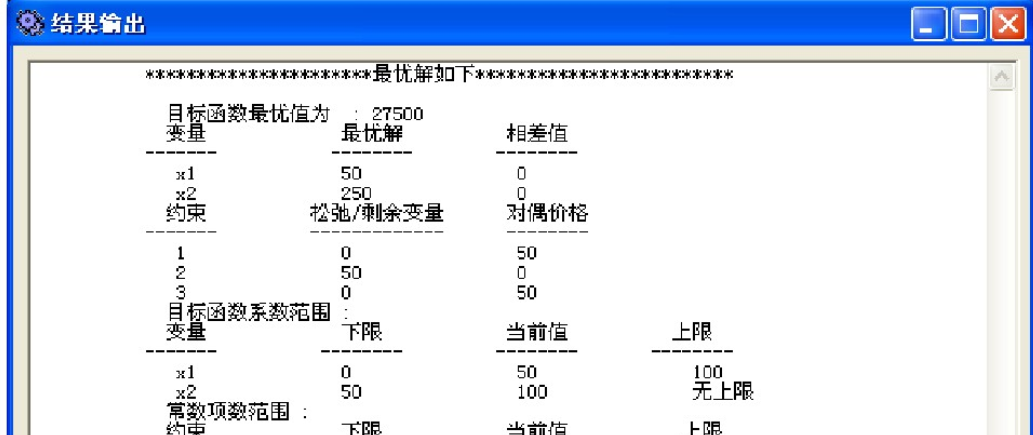
第五步：分析運行結果。

-本題中目標函數的最優(yōu)值是27500，x1=50，X2=250。

-相差值表示相應的決策變量的目標系數需要改進的數量，使得決策變量為正值，當決策變量已為正數時，相差數為零。

一松弛/剩余變量的數值表示還有多少資源沒有被使用。如果為零，則表示與之相對應的資源已經全部用上。