高中數(shù)學(xué)-考點突破：解析幾何-苗金利課程目錄
第1講 直線與圓的方程 P1
（1）直線的傾斜角
定義：x軸正向與直線向上方向之間所成的角叫直線的傾斜角。特別地，當(dāng)直線與x軸平行或重合時，我們規(guī)定它的傾斜角為0°因此，傾斜角的取值范圍是0°≤α<180°
（2）直線的斜率
①定義：傾斜角不是90°的直線，它的傾斜角的正切叫做這條直線的斜率。直線的斜率常用k表示。即k=tanc。
斜率反映直線與軸的傾斜程度。
當(dāng)直線l與x軸平行或重合時，a=0，k=tan0°=0；當(dāng)直線l與x軸垂直時，a=900，k不存在.
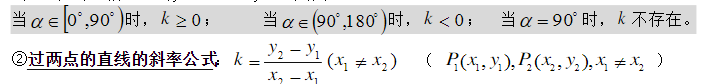
注意下面四點：（1）當(dāng)x=x，時，公式右邊無意義，直線的斜率不存在，傾斜角為90°；
（2）k與P1、P2的順序無關(guān)；
（3）以后求斜率可不通過傾斜角而由直線上兩點的坐標直接求得；
（4）求直線的傾斜角可由直線上兩點的坐標先求斜率得到。
（3）直線方程
@①點斜式：y-y1=k（x-x1）直線斜率k，且過點（G，為）注意：當(dāng)直線的斜率為0°時，k=0，直線的方程是y=y1。
當(dāng)直線的斜率為90°時，直線的斜率不存在，它的方程不能用點斜式表示.但因l上每一點的橫坐標都等于x1，所以它的方程是x=x1。
第1講 直線與圓的方程 P2
第2講 直線與圓的位置關(guān)系 P1
第2講 直線與圓的位置關(guān)系 P2
1.能判斷直線與圓、圓與圓的位置關(guān)系
2.能利用坐標法解決一些簡單的位置關(guān)系基本問題要求
3.理解坐標法解決幾何問題的一般步驟
4.能根據(jù)條件求直線或圓的方程1.通過研究圓上任意一點與直線上任意一點之間距離的最值問題，體會數(shù)形結(jié)合、發(fā)展
化歸的思想方法
要求
2.通過兩圓關(guān)于直線對稱問題的研究，進一步體會解析法思想
I知識梳理m
1.直線與圓的位置關(guān)系
（1）三種位置關(guān)系：相交、相切、相離.
（2）兩種研究方法：
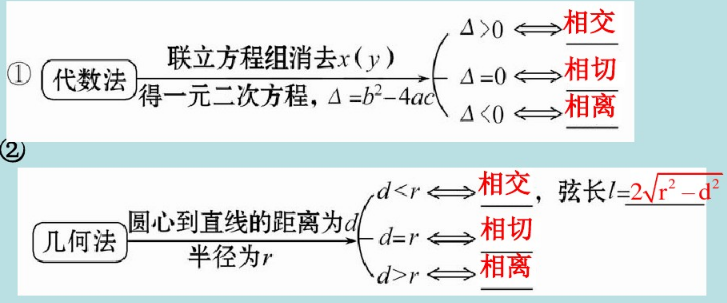
第3講 線性規(guī)劃 P1
第3講 線性規(guī)劃 P2
要點·疑點·考點
1.二元一次不等式表示平面區(qū)域（1）二元一次不等式Ax+By+C>0在平面直角坐標系中表示直線l:Ax+By+C=0一側(cè)所有點組成的平面區(qū)域，直線l應(yīng)畫成虛線，Ax+By+C<0，表示直線l另一側(cè)所有點組成的平面區(qū)域.畫不等式Ax+By+C20（≤0）所表示的平面區(qū)域時，應(yīng)把邊界直線畫成實線。
（2）二元一次不等式組所表示的平面區(qū)域是各個不等式表示的平面點集的交集即各個不等式所表示的平面區(qū)域的公共部分。
2.線性規(guī)劃
（1）對于變量xy的約束條件，都是關(guān)于x，y的一次不等式，稱為線性約束條件，z=f（x，y）是欲達到最值所涉及的變量x，y的解析式，叫做目標函數(shù).當(dāng)f（x，y）是關(guān)于x，y的一次解析式時，z=f（x，y）叫做線性目標函數(shù)。
（2）求線性目標函數(shù)在約束條件下的最值問題稱為線性規(guī)劃問題，滿足線性約束條件的解（x，y）稱為可行解.由所有解組成的集合叫可行域，使目標函數(shù)取得最值的可行解叫最優(yōu)解。
第4講 圓錐曲線 P1
第4講 圓錐曲線 P2
第5講 圓錐曲線 P3
第5講 圓錐曲線 P4
一、方程的曲線：
在平面直角坐標系中，如果某曲線C（看作適合某種條件的點的集合或軌跡）上的點與一個二元方程f（x，y）=0的實數(shù)解建立了如下的關(guān)系：（1）曲線上的點的坐標都是這個方程的解；（2）以這個方程的解為坐標的點都是曲線上的點，那么這個方程叫做曲線的方程；這條曲線叫做方程的曲線。
點與曲線的關(guān)系：若曲線C的方程是f（x，y）=0，則點Po（xo，yo）在曲線C上今（x0，y0）=0；點Po（xo，yo）不在曲線C上令f（x0，y0）=0。
f（%，y%）=0兩條曲線的交點：若曲線C1，C2的方程分別為f（x，y）=0，f2（x，y）=0，.則點Po（xo，y0）是C1，C2的交點今{
.（G，X%）=0方程組有n個不同的實數(shù)解，兩條曲線就有n個不同的交點；方程組沒有實數(shù)解，曲線就沒有交點。
二、圓：
1、定義：點集{M||OM|=r}，其中定點O為圓心，定長r為半徑.
2、方程：（1）標準方程：圓心在c（a，b），半徑為r的圓方程是（x-a）2+（y-b）2=r2圓心在坐標原點，半徑為r的圓方程是x2+y2=r2
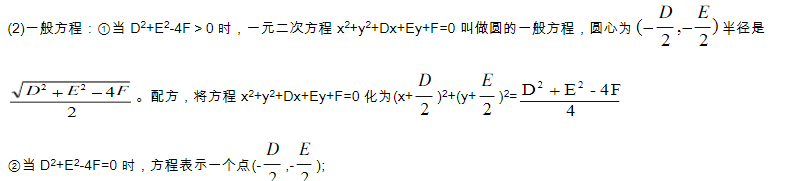三、圓錐曲線的統(tǒng)一定義：
平面內(nèi)的動點P（x，y）到一個定點F（C，0）的距離與到不通過這個定點的一條定直線l的距離之比是一個常數(shù)e（e>0），則動點的軌跡做圓錐曲線。其中定點F（（c，0）稱為焦點，定直線l稱為準線，正常數(shù)e稱為離心率。當(dāng)0
第6講 圓錐曲線綜合 P1
第6講 圓錐曲線綜合 P2
S9.6圓錐曲線的綜合問題
考點一定點與定值問題
1.定點問題
解析幾何中證明直線過定點，一般是先選擇一個參數(shù)建立直線系方程，然后再根據(jù)直線系方程過定點時方程的成立與參數(shù)沒有關(guān)系得到一個關(guān)于x，y的方程組，以這個方程組的解為坐標的點就是直線所過的定點.
2.定值問題
（1）解析幾何中的定值問題的證明可運用函數(shù)的思想方法.證明過程可總結(jié)為“變量函數(shù)→定值”，具體操作步驟如下：
（i）變量——選擇適當(dāng)?shù)牧繛樽兞浚?/p>
（ii）函數(shù)——把要證明為定值的量表示成上述變量的函數(shù)；
（i）定值—把得到的函數(shù)解析式化簡，消去變量得到定值.
（2）求定值問題常見的方法
（i）從特殊入手，求出定值，再證明這個值與變量無關(guān).
（ii）直接推理、計算，并在推理、計算的過程中消去變量，從而得到定值.
