課程目錄：

第1講 函數(shù)與微積分初步 P1

第1講 函數(shù)與微積分初步 P2

第2講 函數(shù)與微積分初步 P3

第2講 函數(shù)與微積分初步 P4

A微積分初步

S1函數(shù)及其圖形

一、函數(shù)、自變量和因變量

1.函數(shù)：如果有兩個(gè)相互聯(lián)系的變量x和y，每當(dāng)變量x取定某個(gè)值以后，按照一定的規(guī)律就可確定y的對(duì)應(yīng)值，我們就稱y是x的函數(shù)，記為y=f（x）（f是函數(shù)記號(hào)表示和間的對(duì)應(yīng)關(guān)系或：y=y（）

2.自變量和因變量：

x：為自變量。x的變化范圍：函數(shù)的定義域。

y：為因變量。y所有取值范圍：函數(shù)的值域。

物理學(xué)中函數(shù)與自變量視研究問(wèn)題而定。例：PV=nRT中可以有兩個(gè)變量；但若V

b.任意常數(shù)：a，b，c等。任意常數(shù)需要通過(guò)具體問(wèn)題確定。常用確定方法：求斜率、截距的方法；非線性函數(shù)先進(jìn)行變量變換，線性化后求斜率、截距的方法等。知道了函數(shù)的形式以后，即可確定與自變量任一特定值對(duì)應(yīng)的函數(shù)值f（x。）。例：

二、函數(shù)的圖形

圖形優(yōu)點(diǎn)：直觀了解一個(gè)函數(shù)的特征；通過(guò)作圖可以擬合物理規(guī)律。

1.平面中的曲線可以表示幾何學(xué)或物理學(xué)中兩變量間的函數(shù)關(guān)系2.作圖方法：（1）逐點(diǎn)描跡的方法。①給一個(gè)x值，求對(duì)應(yīng)的f（x）值，確定（x，y）②實(shí)

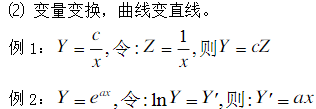
這種方法對(duì)于確定任意常數(shù)極為方便，是實(shí)驗(yàn)中常用方法之一。

3.二元函數(shù)的圖形是三維空間中的曲面

三、物理學(xué)中函數(shù)實(shí)例：

反映任何一個(gè)物理規(guī)律的公式都是表達(dá)變量與變量之間的函數(shù)關(guān)系。

1.勻速直線運(yùn)動(dòng)公式V=常數(shù)

s=So+Vl，s=S）。反映了位置隨時(shí)間的變化規(guī)律。so，v為任意常數(shù)，s。為初位置，v速度，s。與坐標(biāo)原點(diǎn)選擇有關(guān)，v對(duì)每個(gè)勻速直線運(yùn)動(dòng)有一定值，對(duì)不同的勻速直線運(yùn)動(dòng)可以取不同的值。

2.勻變速直線運(yùn)動(dòng)公式

結(jié)論：自變量、因變量與常數(shù)，有時(shí)從公式本身并不能明確反映不出來(lái)，需要由具體問(wèn)題分析確定。

第3講 三角函數(shù)概念圖像性質(zhì) P1 

第3講 三角函數(shù)概念圖像性質(zhì) P2 

考試內(nèi)容

任意角的概念和弧度制

弧度與角度的互化

任意角的正弦、余弦、正切的定義用單位圓中的三角函數(shù)線表示正弦、余弦和正切誘導(dǎo)公式

同角三角函數(shù)的基本關(guān)系式

周期函數(shù)的定義、三角函數(shù)的周期性函數(shù)y=sinx，y=cosx，y=tanx的圖象和性質(zhì)

函數(shù)y=Asin（ox+9）的圖象用三角函數(shù)解決一些簡(jiǎn)單的實(shí)際問(wèn)題

用三角函數(shù)解決一些簡(jiǎn)單的實(shí)際問(wèn)題

兩角和與差的正弦、余弦、正切公式

二倍角的正弦、余弦、正切公式

簡(jiǎn)單的恒等變換

正弦定理、余弦定理

解三角形

第4講 三角函數(shù)公式與綜合應(yīng)用 P1

第4講 三角函數(shù)公式與綜合應(yīng)用 P2

高考對(duì)三角恒等式部分的考查仍會(huì)是中低檔題，無(wú)論是小題還是大題中出現(xiàn)都是較容易的.主要有三種可能：

（1）以小題形式直接考查：利用兩角和與差以及二倍角公式求值、化簡(jiǎn)；

（2）以小題形式與三角函數(shù)、向量、解三角形等知識(shí)相綜合考查兩角和與差以及二倍角等公式；

（3）以解答題形式與三角函數(shù)、向量、解三角形、函數(shù)等知識(shí)相綜合考查，對(duì)三角恒等變換的綜合應(yīng)用也可能與解三角形一起用于分析解決實(shí)際問(wèn)題的應(yīng)用問(wèn)題，主要考查綜合運(yùn)用數(shù)學(xué)知識(shí)分析問(wèn)題和解決問(wèn)題的能力。

復(fù)習(xí)時(shí)，要注重對(duì)間題中角、函數(shù)名及其整體結(jié)構(gòu)的分析，提高公式選擇的恰當(dāng)性，還要重視相關(guān)的思想方法，如數(shù)形結(jié)合思想、特值法、構(gòu)造法、等價(jià)轉(zhuǎn)換法等的總結(jié)和應(yīng)用，這有利于縮短運(yùn)算程序，提高解題效率。

【知識(shí)升華】

1.三角函數(shù)的化簡(jiǎn)與求值、證明的難點(diǎn)在于眾多三角公式的靈活運(yùn)用和解題突破口的合理選擇，要認(rèn)真分析所給式子的整體結(jié)構(gòu)，分析各個(gè)三角函數(shù)及角的相互關(guān)系是靈活選用公式的基礎(chǔ)，是恰當(dāng)尋找解題思維起點(diǎn)的關(guān)鍵所在。

（1）化簡(jiǎn)，要求使三角函數(shù)式成為最簡(jiǎn)：項(xiàng)數(shù)盡量少，名稱盡量少，次數(shù)盡量底，分母盡量不含三角函數(shù)，根號(hào)內(nèi)盡量不含三角函數(shù)，能求值的求出值來(lái)；

（2）求值，要注意象限角的范圍、三角函數(shù)值的符號(hào)之間聯(lián)系與影響，較難的問(wèn)題需要根據(jù)上三角函數(shù)值進(jìn)一步縮小角的范圍。

（3）證明是利用恒等變換公式將等式的左邊變同于右邊，或右邊變同于，或都將左右進(jìn)行變換使其左右相等。

第5講 等差、等比數(shù)列 P1

第5講 等差、等比數(shù)列 P2

第6講 數(shù)列的綜合 P1

第6講 數(shù)列的綜合 P2

知識(shí)梳理

1.數(shù)列的通項(xiàng)求數(shù)列通項(xiàng)公式的常用方法：

（1）觀察與歸納法：先觀察哪些因素隨項(xiàng)數(shù)1的變化而變化，哪些因素不變：分析符號(hào)、數(shù)字、字母與項(xiàng)數(shù)n在變化過(guò)程中的聯(lián)系，初步歸納公式。

（2）公式法：等差數(shù)列與等比數(shù)列。

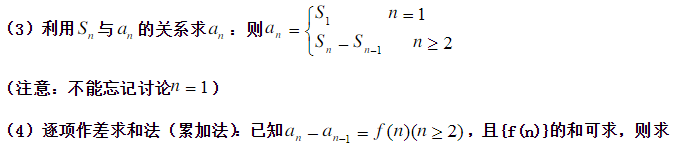
3.數(shù)列求和的常用方法：

（1）公式法：①等差數(shù)列求和公式；②等比數(shù)列求和公式（2）分組求和法：在直接運(yùn)用公式法求和有困難時(shí)，常將“和式”中“同類(lèi)項(xiàng)”先合并在一起，再運(yùn)用公式法求和

（3）倒序相加法：在數(shù)列求和中，若和式中到首尾距離相等的兩項(xiàng)和有其共性或數(shù)列的通項(xiàng)與組合數(shù)相關(guān)聯(lián)，則常可考慮選用倒序相加法，發(fā)揮其共性的作用求和（這也是等差數(shù)列前n和公式的推導(dǎo)方法）.

（4）錯(cuò)位相減法：如果數(shù)列的通項(xiàng)是由一個(gè)等差數(shù)列的通項(xiàng)與一個(gè)等比數(shù)列的通項(xiàng)相乘構(gòu)成，那么常選用錯(cuò)位相減法，將其和轉(zhuǎn)化為“一個(gè)新的的等比數(shù)列的和”求解（注意：

一般錯(cuò)位相減后，其中“新等比數(shù)列的項(xiàng)數(shù)是原數(shù)列的項(xiàng)數(shù)減一的差）（這也是等

（5）裂項(xiàng)相消法：如果數(shù)列的通項(xiàng)可“分裂成兩項(xiàng)差”的形式，且相鄰項(xiàng)分裂后相關(guān)聯(lián)，那么常選用裂項(xiàng)相消法求和常用裂項(xiàng)形式有：

第7講 數(shù)列綜合與算法初步 P1

第7講 數(shù)列綜合與算法初步 P2

第8講 平面向量及空間向量 P1

第8講 平面向量及空間向量 P2

向量及運(yùn)算是現(xiàn)代數(shù)學(xué)重要標(biāo)志之一，其引入給中學(xué)數(shù)學(xué)帶來(lái)了無(wú)限生機(jī)和活力，大大拓寬了解題的思路與方法。它以平面幾何、直角坐標(biāo)系、三角函數(shù)等知識(shí)為基礎(chǔ)，融數(shù)、形于一體，它已成為中學(xué)數(shù)學(xué)知識(shí)的一個(gè)交匯點(diǎn)。因此，向量是高考命題中“在知識(shí)網(wǎng)絡(luò)處設(shè)計(jì)試題”的很好載體。

一、考試要求解讀

1.平面向量：（考試要求）

（1）理解向量的概念，掌握向量的幾何表示，了解共線向量的概念；

（2）掌握向量加法與減法；

（3）掌握實(shí)數(shù)與向量的積，理解兩個(gè)向量共線的充要條件；

（4）了解平面向量的基本定理，理解平面向量的坐標(biāo)的概念，掌握平面向量的坐標(biāo)運(yùn)算；

（5）掌握平面向量的數(shù)量積及其幾何意義，了解用平面向量的數(shù)量積可以處理有關(guān)長(zhǎng)度、角度和垂直的問(wèn)題，掌握向量垂直的條件；

（6）掌握平面兩點(diǎn)間的距離公式，以及線段的定比分點(diǎn)和中點(diǎn)坐標(biāo)公式，并且能熟練運(yùn)用，掌握平移公式；

三、典型例題分析

（1）注意平面向量與三角知識(shí)的聯(lián)系；

（2）重視以平面向量為背景的解幾命題趨勢(shì)；

（3）重視向量為工具處理立體幾何問(wèn)題；

（4）構(gòu)造向量，探索解題新思路。