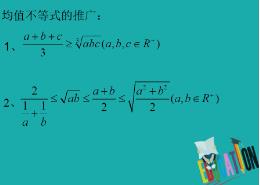高中數(shù)學(xué)中常見(jiàn)的不等式解法方法有以下十四種:
代數(shù)法:通過(guò)代數(shù)運(yùn)算將不等式化簡(jiǎn)為更容易處理的形式。
分段討論法:將不等式分成若干段,分別討論每個(gè)段的情況。
加減變形法:通過(guò)加減變形使得不等式更容易處理。
乘除變形法:通過(guò)乘除變形使得不等式更容易處理。
變量替換法:通過(guò)替換變量引入新的不等式形式。
幾何法:將不等式轉(zhuǎn)化為幾何問(wèn)題,利用幾何性質(zhì)解決。
拆分法:將不等式中的復(fù)雜項(xiàng)拆分成簡(jiǎn)單項(xiàng)處理。
倒置法:將不等式倒置處理,有時(shí)候更容易求解。
奇偶性討論法:通過(guò)奇偶性討論不等式的性質(zhì)。
整式化簡(jiǎn)法:將不等式中的復(fù)雜整式化簡(jiǎn)為簡(jiǎn)單整式處理。
三角函數(shù)法:通過(guò)三角函數(shù)的性質(zhì)解決不等式。
極值法:通過(guò)求函數(shù)的極值來(lái)討論不等式的情況。
積分法:通過(guò)積分來(lái)討論不等式的情況。
數(shù)學(xué)歸納法:通過(guò)數(shù)學(xué)歸納法證明不等式的成立。
這些方法在解決高中數(shù)學(xué)中的不等式問(wèn)題時(shí)經(jīng)常會(huì)用到,學(xué)生在掌握這些方法的同時(shí),也需要靈活應(yīng)用,根據(jù)具體問(wèn)題選擇合適的方法進(jìn)行求解。