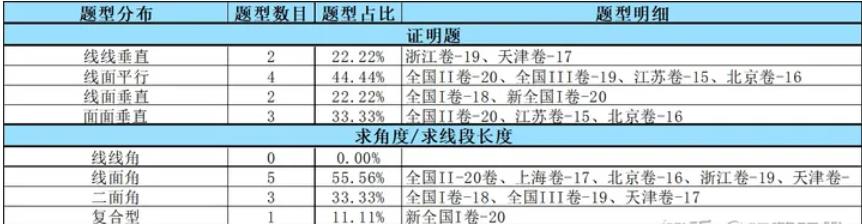
一、低難度

9道立體幾何大題中其中以江蘇卷和上海卷的題目較為簡單。江蘇卷考察的是三棱柱，上海卷考察的是正方體，兩道題證明簡單且計(jì)算量較小。下面逐一進(jìn)行精講：

二、中難度

9道立體幾何大題中全國I卷、全國III卷、北京卷、天津卷4道大題難度適中，計(jì)算量適中，題目設(shè)置中規(guī)中矩，均屬于常見題型。主要涉及三棱錐、長方體、正方體和直三棱柱。題目中均容易找到互相垂直的三個(gè)平面，容易構(gòu)建空間直角坐標(biāo)系，但要保障計(jì)算的準(zhǔn)確度。下面逐一進(jìn)行精講：

三、高難度

9道立體幾何大題中全國II卷、新全國I卷、浙江卷3道大題難度較大，計(jì)算量較大，全國II卷的難點(diǎn)主要在于空間直角坐標(biāo)系難以構(gòu)建，各點(diǎn)坐標(biāo)難以直接表示；新全國I卷的難點(diǎn)主要體現(xiàn)在將線面角大小與均值不等式求極值相結(jié)合，增大了計(jì)算量和整體難度；浙江卷的考的是不常見的三棱臺，難點(diǎn)主要體現(xiàn)兩方面：一是空間直角坐標(biāo)系構(gòu)建困難，空間坐標(biāo)表示復(fù)雜，二是證明部分由于題干中并未直接給出位置條件，而是給出了角度關(guān)系和線段長度關(guān)系，因此需要采用解三角形的方法，通過求角度大小來證明垂直。下面逐一進(jìn)行精講：

四、總結(jié)

本期我們主要是對2020年高考題中涉及到的與立體幾何相關(guān)的9道大題進(jìn)行了精講，整體上來看并不大，難度梯度明顯，但值得注意的是部分試卷已經(jīng)開始將立體幾何作為準(zhǔn)壓軸題，并且將立體幾何的考點(diǎn)與解三角形以及不等式考點(diǎn)相結(jié)合，大大增加了考點(diǎn)的覆蓋范圍。此外也增加了對棱臺和斜棱柱等不容易直接構(gòu)建空間直接坐標(biāo)系的幾何體的考察。

五、下期預(yù)告

下周正男老師將繼續(xù)回歸對立體幾何主要考點(diǎn)的梳理及精講，下一個(gè)專題為立體幾何小題的球/圓柱/圓錐專題，并從命題者角度出發(fā)，幫助各位考生識破該類題型的主要考點(diǎn)，希望可以幫助各位同學(xué)，敬請期待！有興趣的同學(xué)可以關(guān)注我的微信公眾號——正男的數(shù)學(xué)課堂，或者加我的個(gè)人微信：gongtengzhengnan，謝謝大家！