課程目錄:
第1講 線面關(guān)系(上)
第1講 線面關(guān)系(下)
1、直線與直線的位置關(guān)系:
(1)相交直線一一兩直線在同一平面內(nèi),兩直線有且僅有一個公共點。
(2)平面直線一-兩直線在同一平面內(nèi),兩直線沒有公共點。
(3)異面直線一-不存在一個平面同時經(jīng)過這兩條直線。
過平面外一點與平面內(nèi)一點的直線,和平面內(nèi)不經(jīng)過該點的直線異面。
2、直線與平面的位置關(guān)系:
(1)直線在平面內(nèi):直線上兩點在一個平面內(nèi),那么此直線上所有點都在平面內(nèi)。
(2)直線在平面外:①直線和平面平行。②直線和平面相交。兩條平行線中一條與已知平面相交,則另一條也與該平面相交。
3、平面和平面的位置關(guān)系:
(1)平行一一沒在公共點。
(2)相交—一至少有一公共點(或一公共直線)。
如果兩個平面內(nèi)分別有一條直線,這兩條直線互相平行,那么這兩個平面一定是平行或相交。
3、平面和平面的位置關(guān)系:
(1)平行一一沒在公共點。
(2)相交一一至少有一公共點(或一公共直線)。
如果兩個平面內(nèi)分別有一條直線,這兩條直線互相平行,那么這兩個平面一定是平行或相交。
4、直線和平面平行的判定定理:
如果平面外一條直線和這個平面內(nèi)的一條直線平行,那么這條直線和這個平面平行。
5、直線和平面平行的性質(zhì)定理:
一條直線與一個平面平行,則過這條直線的任一平面和此平面的交線與該直線平行。
6、平面與平面平行的判定定理:
(1)如果一個平面內(nèi)的兩條相交直線都平行于另一平面,那么這兩個平面平行。
(2)如果一個平面內(nèi)兩條相交直線分別平行于另一個平面內(nèi)的兩條相交直線,則這兩個平面平行。
第2講 空間幾何體(上)
第2講 空間幾何體(下)
一、空間幾何體的結(jié)構(gòu)特征
1.柱、錐、臺、球的結(jié)構(gòu)特征
由若干個平面多邊形圍成的幾何體稱之為多面體。圍成多面體的各個多邊形叫叫做多面體的面,相鄰兩個面的公共邊叫做多面體的棱,棱與棱的公共點叫做頂點。
把一個平面圖形繞它所在平面內(nèi)的一條定直線旋轉(zhuǎn)形成的封閉幾何體稱之為旋轉(zhuǎn)體,其中定直線稱為旋轉(zhuǎn)體的軸。
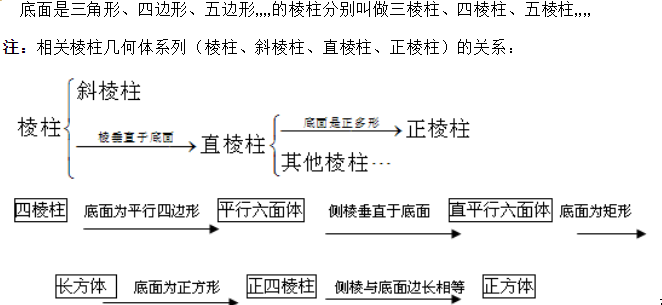
(1)柱
棱柱:一般的,有兩個面互相平行,其余各面都是四邊形,并且每相鄰兩個四邊形的公共邊都互相平行,由這些面所圍成的幾何體叫做棱柱;棱柱中兩個互相平行的面叫做棱柱的底面,簡稱為底;其余各面叫做棱柱的側(cè)面;相鄰側(cè)面的公共邊叫做棱柱的側(cè)棱;側(cè)面與底面的公共頂點叫做棱柱的頂點。
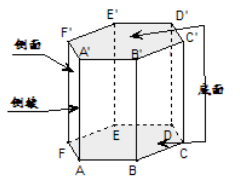
①側(cè)棱都相等,側(cè)面是平行四邊形;
②兩個底面與平行于底面的截面是全等的多邊形;
③過不相鄰的兩條側(cè)棱的截面是平行四邊形;
④直棱柱的側(cè)棱長與高相等,側(cè)面與對角面是矩形。
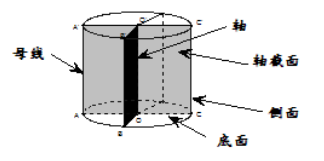
圓柱:以矩形的一邊所在的直線為旋轉(zhuǎn)軸,其余邊旋轉(zhuǎn)形成的曲面所圍成的幾何體叫做圓柱;旋轉(zhuǎn)軸
叫做圓柱的軸;垂直于軸的邊旋轉(zhuǎn)而成的曲面叫做圓柱的側(cè)面;無論旋轉(zhuǎn)到什么位置,不垂直于軸的邊都叫做圓柱側(cè)面的母線。
第3講 排列、組合(上)
第3講 排列、組合(下)
排列組合問題聯(lián)系實際生動有趣,但題型多樣,思路靈活,因此解決排列組合問題,首先要認真審題,弄清楚是排列問題、組合問題還是排列與組合綜合問題;其次要抓住問題的本質(zhì)特征,采用合理恰當?shù)姆椒▉硖幚怼?/strong>
分類計數(shù)原理(加法原理)完成一件事,有n類辦法,在第1類辦法中有m種不同的方法,在第2類辦法中有mm種不同的方法,,,在第n類辦法中有m種不同的方法,那么完成這件事共有:
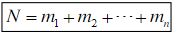
種不同的方法.
2.分步計數(shù)原理(乘法原理)完成一件事,需要分成n個步驟,做第1步有m種不同的方法,做第2步有mm種不同的方法,,,做第n步有m,種不同的方法,那么完成這件事共有:
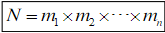
種不同的方法.
3.分類計數(shù)原理分步計數(shù)原理區(qū)別
分類計數(shù)原理方法相互獨立,任何一種方法都可以獨立地完成這件事。分步計數(shù)原理各步相互依存,每步中的方法完成事件的一個階段,不能完成整個事件.
解決排列組合綜合性問題的一般過程如下:
1.認真審題弄清要做什么事
2.怎樣做才能完成所要做的事,即采取分步還是分類,或是分步與分類同時進行,確定分多少步及多少類。
3.確定每一步或每一類是排列問題(有序)還是組合(無序)問題,元素總數(shù)是多少及取出多少個元素.
4.解決排列組合綜合性問題,往往類與步交叉,因此必須掌握一些常用的解題策略
第4講 二項式定理 P1
第4講 二項式定理 P2
$10.5二項式定理理解二須式定理,會利用二項式定理求二項脫開式
掌握二項展開式的通項公式,會應(yīng)用通項公式求指定的一項,E會正確區(qū)分二項式系數(shù)與項的系數(shù),會求指定須的二項式系數(shù)和系數(shù)。


第4講 二項式定理 P3
第5講 概率與統(tǒng)計 P1
第5講 概率與統(tǒng)計 P2
第6講 P3
第6講 概率與統(tǒng)計 P4
一.算法,概率和統(tǒng)計
1.算法初步(約12課時)(1)算法的含義、程序框圖
①通過對解決具體問題過程與步驟的分析(如,二元一次方程組求解等問題),體會算法的思想,了解算法的含義。
②通過模仿、操作、探索,經(jīng)歷通過設(shè)計程序框圖表達解決問題的過程。在具體問題的解決過程中(如,三元一次方程組求解等問題),理解程序框圖的三種基本邏輯結(jié)構(gòu):順序、條件分支、循環(huán)。
(2)基本算法語句
經(jīng)歷將具體問題的程序框圖轉(zhuǎn)化為程序語句的過程,理解幾種基本算法語句--輸入語句、輸出語句、賦值語句、條件語句、循環(huán)語句,進一步體會算法的基本思想。
(3)通過閱讀中國古代數(shù)學(xué)中的算法案例,體會中國古代數(shù)學(xué)對世界數(shù)學(xué)發(fā)展的貢獻。
3.概率(約8課時)
(1)在具體情境中,了解隨機事件發(fā)生的不確定性和頻率的穩(wěn)定性,進一步了解概率的意義以及頻率與概率的區(qū)別。
(2)通過實例,了解兩個互斥事件的概率加法公式。
(3)通過實例,理解古典概型及其概率計算公式,會用列舉法計算一些隨機事件所含的基本事件數(shù)及事件發(fā)生的概率。