1.1畫法幾何學的任務

1.1.1本課程的性質和任務

工程圖樣是表達和交流技術思想的重要工具。在現代工業(yè)中，設計和制造機床、車輛、船舶、采礦與冶金設備、化工設備、各種儀表或電子儀器等，都必須先畫出圖樣，然后根據圖紙加工，才能得到預想的結果。在使用這些機器、設備和儀表時，也常常要通過閱讀圖樣來了解它們的結構和性能。所以我們說：“工程圖樣是工程界的技術語言”。每一個工程技術人員，如果不能熟練掌握它，是無法勝任工程設計和科研工作的。作為一個工科高等學校的學生，掌握繪制工程圖樣的基本理論和方法，是今后從事設計、制造和加工以及科學研究工作的基本技能之一。

畫法幾何學是研究如何在平面上圖示空間物體和圖解空間幾何問題的一門學科，它為繪制工程圖樣提供了基本原理和基本方法。并且為正確地圖解空間幾何問題提供了理論基礎、為用平面圖樣完整地表達出空間物體，提供了理論依據。

學習畫法幾何學的任務和目的主要有以下幾點：

（1）學習平行投影的基本理論，特別是正投影法的原理和應用；

（2）學習用平面圖形表達空間幾何形體的圖示法；

（3）熟練掌握空間幾何元素的定位問題和度量問題的圖解法；

（4）培養(yǎng)空間邏輯思維和空間想象能力；

（5）培養(yǎng)耐心細致的工作風和認真負責的工作態(tài)度。

1.1.2本課欄的字習萬法

畫法幾何學的理論具有完整性和系統(tǒng)性，它的課程學習有一個鮮明的特點：用作圖來培養(yǎng)空間邏輯思維和想象能力。即在學習的過程中，始終必須將平面上的投影與想象的空間幾何元素結合起來。這種平面投影分析與空間形體想象的結合，是二維思維與三維思維間的轉換。而這種轉換能力的培養(yǎng)，只能逐步做到。

在學習中，應遵循下述學習方法：

（1）認真聽課，及時復習，正確理解基本原理，掌握基本方法，注意領會例題所示的分析方法和作圖過程。注意物體與圖樣之間的關系，逐步提高自己的空間思維能力和空間分析能力。

（2）繪圖技能的培養(yǎng)和空間思維能力的提高，都需要通過一定數量的練習來實現，因此要嚴肅認真地對待每一道習題和每一次繪圖訓練。作業(yè)不僅要求正確，而且要求整潔、清晰。

（3）由于圖樣在生產實踐中起著很重要的作用，繪圖和讀圖的任何差錯，都會給生產造成損失，因此在繪圖和讀圖時要細致和耐心，做到一絲不茍，仔細認真。

1.2投影法

1.2.1投影法的基本知識

在日常生活中，燈光和陽光照射物體時，會在地面、墻面上產生影子。人們把這種投影現象加以抽象，總結出投影理論后，用以解決物和圖的轉換問題。

1.中心投影

圖1-1所示，設空間有電燈、三角形ABC和一平面P。燈光照射到被投影物（三角板）ABC在P面上留下影子abc。我們稱s為投射中心、P為投影面、ABC為被投影的空間物體。

光源、被投影物和投影平面是進行投影時不可缺少的條件，通常稱為投影三要素。上述現象可抽象為經s和A、B、C各作一條直線SA、SB、SC（SA、SB、SC稱為投射線），與P平面分別交于a、b、c三點。a、b、c三點就是空間A、B、C三點在P平面上的投影。這種投射線都通過投影中心s點投影，稱為中心投影。同時規(guī)定，空間點用大寫字母表示，投影點用同名稱的小寫字母表示。

2.平行投影

將中心投影中的中心S移向無窮遠，則投射線相互平行。這種投射線相互平行的投影，稱為平行投影。平行投影又分為斜投影和正投影，前者投射線與投影面傾斜（圖1-2），后者投射線與投影面垂直（圖1-3）。

投射線相互平行、且都垂直于投影面的投影稱為正投影，它被廣泛地用作為工程上“物一圖”轉換的工具。

1.2.2空間幾何原形與其投影間的對應問題1.畫法幾何及其投影法主要研究空間幾何原形與其投影之間的對應關系，即研究他們之間內在聯系的規(guī)律性。其研究途徑無非是討論投影圖上仍保持了哪些空間幾何關系不變，而哪些幾何關系有了變化和形成怎樣的變化。尤其是要掌握住那些不變的關系，作為畫圖和看圖的基本依據。

例如，平行投影有這樣的規(guī)律：

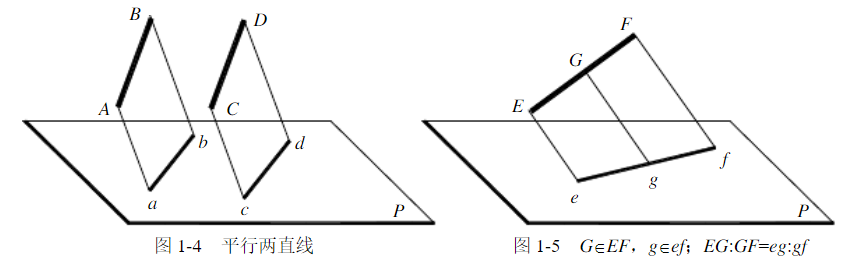
（1）平行兩直線的投影仍相互平行：如圖1-4，AB//CD，則abllcd。

（2）屬于直線上的點，其投影仍屬于直線的投影：如圖1-5中的G點。

（3）點分線段之比，投影后保持不變：如圖1-5，EG:GF=eg:g/

上述規(guī)律，均可用初等幾何的知識得到證明。

2.工程上用的投影圖，必須能確切地惟一的反映出空間的幾何關系。前面只說明了有可能用一些投影規(guī)律來確定投影圖。反過來，能否根據投影圖惟一的確定空間幾何關系呢？事實上，只憑一個投影，不能反映惟一空間情況。例如，圖1-6，投影圖上有相互平行的兩直線ab//cd，但對應到空間可能是相互平行兩直線，如圖1-4；也可能是不平行的兩直線AB和CD，如圖1-6。又如圖1-7，投影圖上點h屬于線段ef，即heef。但對應到空間的點H，可能是屬于線段EF，也可能不屬于線段EF，即可能HeEF，也可能HgEF。再如圖1-8，投影面上的圖像所表示的可能是幾何體1，可能是幾何體Ⅱ，還可能是其他形狀的幾何體。這是因為一個空間點有惟一確定的投影，每一條確定的投射線與投影面只能交于一點。如圖1-1A點，但點的一個投影不能確定該點的空間位置，如圖1-9，當投射方向確定時，投影a可以對應投射線上的任意點A1、A2、A3、…，也就是空間的點是不確定的。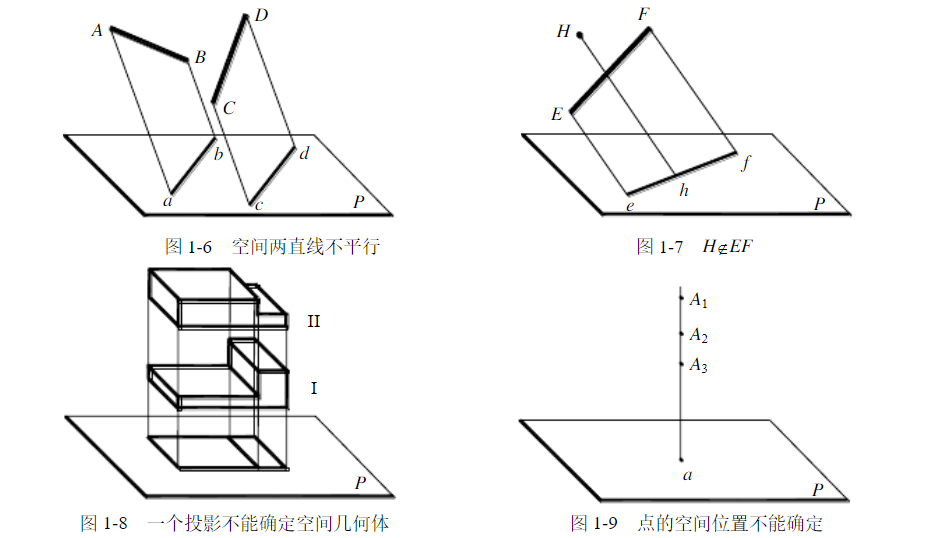

既然要求投影圖能確切、惟一的反映空間的幾何關系，就需再引入一些條件和規(guī)定來滿足這個問題。因而在工程上根據不同情況分別作了一些專門規(guī)定，相應地形成了若干投影方法，如正投影法、軸測投影法、標高投影法和透視投影法等等。機械制造業(yè)用得最廣泛的是正投影法，也常采用軸測投影法。

1.2.3常用工程圖

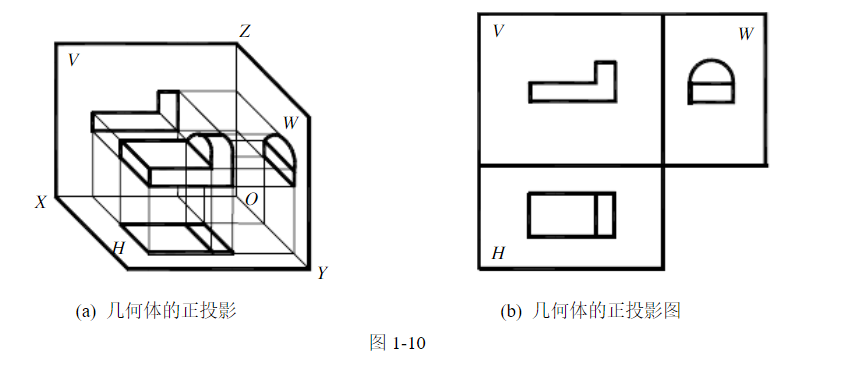
1.多面正投影圖

圖1-10（a）表示工程上常見的用正投影法作出三視圖的原理，它是典型的多面視圖的例子。由于三視圖（圖1-10（b））真實地表達了零件的內外部結構和形狀，配以尺寸標注和其他技術要求后，完全滿足了機械加工的要求。