一、課程目標
本課程旨在讓學員在短時間內掌握 Matlab 的核心功能,以便能夠運用 Matlab 進行數學建模,解決實際問題。通過理論講解和案例實踐,學員將學會數據處理、算法實現和模型求解等關鍵步驟,最終能夠獨立完成簡單到中等復雜程度的數學建模項目。
二、課程內容
(一)Matlab 基礎入門(1 - 2 天)
Matlab 界面介紹
講解 Matlab 的主窗口、命令窗口、工作區(qū)、編輯器等主要界面組成部分。例如,在命令窗口中可以直接輸入命令進行簡單的計算,如輸入 “2+3” 并回車,就會立即得到結果 “5”。
介紹如何設置工作路徑,方便文件的保存和讀取。工作路徑就像是一個文件存儲的文件夾,Matlab 會默認在這個路徑下尋找和保存文件。
基本數據類型和變量
詳細講解 Matlab 中的基本數據類型,包括數值型(如單精度、雙精度)、字符型、邏輯型等。例如,定義一個數值型變量 “a = 3.14;”,一個字符型變量 “b = 'hello';”。
變量的命名規(guī)則和賦值操作。變量名必須以字母開頭,后面可以跟數字和下劃線,不能包含空格和特殊字符。賦值操作可以使用 “=” 符號,如 “x = 10;”。
常用數學運算和函數
算術運算(加、減、乘、除、冪運算)的符號和優(yōu)先級。例如,“34+2” 先計算乘法 “34 = 12”,再計算加法 “12+2 = 14”。
介紹一些常用的數學函數,如三角函數(sin、cos、tan)、對數函數(log、log10)、指數函數(exp)等。例如,計算正弦函數 “sin (pi/2)”(pi 是 Matlab 中預定義的圓周率常量),結果為 “1”。
(二)數據處理與可視化(2 - 3 天)
數據讀取和存儲
講解如何從外部文件(如文本文件、Excel 文件)中讀取數據。對于文本文件,可以使用 “l(fā)oad” 函數(適用于簡單的數值數據)或 “textread” 函數(更靈活的文本數據讀取)。對于 Excel 文件,可以使用 “xlsread” 函數。
數據存儲操作,包括將 Matlab 中的數據保存為文本文件或其他格式。例如,使用 “save” 函數將數據保存為.mat 文件,方便下次使用。
數據預處理
數據清洗,如去除重復數據、處理缺失數據。對于缺失數據,可以采用刪除含有缺失值的行或列,或者使用均值、中位數等統(tǒng)計量填充缺失值。
數據標準化和歸一化操作。標準化可以將數據轉換為均值為 0、標準差為 1 的分布,使用公式 “(x - mean (x))/std (x)”;歸一化可以將數據映射到特定區(qū)間,如 [0,1] 區(qū)間,使用公式 “(x - min (x))/(max (x)-min (x))”。
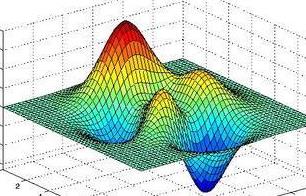
數據可視化
介紹 Matlab 中基本的繪圖函數,如 “plot”(用于繪制折線圖)、“scatter”(用于繪制散點圖)、“bar”(用于繪制柱狀圖)等。例如,使用 “x = 1:10; y = sin (x); plot (x,y)” 可以繪制出正弦函數在 1 到 10 區(qū)間的折線圖。
圖形的修飾,包括添加標題、坐標軸標簽、圖例等。可以使用 “title” 函數添加標題,“xlabel” 和 “ylabel” 函數添加坐標軸標簽,“l(fā)egend” 函數添加圖例。
(三)算法實現與模型構建(3 - 4 天)
常用算法實現
簡單算法,如排序算法(冒泡排序、快速排序)。以冒泡排序為例,通過相鄰元素的比較和交換,將數列從小到大排序。代碼示例:
matlab
復制
function sortedArray = bubbleSort(array)
n = length(array);
for i = 1:n - 1
for j = 1:n - i
if array(j)>array(j + 1)
temp = array(j);
array(j) = array(j + 1);
array(j + 1) = temp;
end
end
end
sortedArray = array;
end
數值計算算法,如牛頓迭代法求解方程的根。牛頓迭代法的基本思想是通過迭代公式 “x (n+1)=x (n)-f (x (n))/f'(x (n))” 來逼近方程的根。
數學模型構建基礎
線性回歸模型。介紹如何使用 Matlab 建立簡單的線性回歸模型,包括最小二乘法求解回歸系數。例如,對于一組數據點 “(x (i),y (i))”,假設線性回歸模型為 “y = a*x + b”,可以通過計算得到回歸系數 “a” 和 “b”,使得預測值與實際值的誤差平方和最小。
簡單的優(yōu)化模型,如線性規(guī)劃問題。在 Matlab 中可以使用 “l(fā)inprog” 函數求解線性規(guī)劃問題,包括定義目標函數、約束條件等。例如,對于目標函數 “z = c'x”,約束條件 “Ax <= b” 等線性規(guī)劃問題進行求解。
(四)數學建模案例實踐(3 - 4 天)
案例分析與講解
選擇經典的數學建模案例,如人口增長模型(如馬爾薩斯人口模型、Logistic 人口模型)。以 Logistic 人口模型為例,講解模型的假設、方程的建立(“dN/dt = rN(1 - N/K)”,其中 N 是人口數量,r 是增長率,K 是環(huán)境容納量),以及在 Matlab 中的實現和參數估計方法。
資源分配模型,如生產計劃安排問題。分析如何將有限的資源(如原材料、勞動力)分配到不同的產品生產中,以達到最大利潤或最小成本的目標。在 Matlab 中通過建立目標函數和約束條件,利用優(yōu)化算法進行求解。
學員實踐操作
學員分組進行案例實踐,根據給定的實際問題,運用所學的 Matlab 知識進行數學建模。例如,給定一個交通流量預測問題,學員需要收集數據、建立合適的預測模型(如時間序列模型),并在 Matlab 中實現和驗證模型。
教師對學員的實踐操作進行指導和點評,幫助學員解決在建模過程中遇到的問題,如模型選擇不當、算法實現錯誤等。
三、課程總結與復習
總結 Matlab 數學建模的關鍵知識點,包括數據處理、算法實現、模型構建等方面。
復習重要的函數和操作,如繪圖函數、數據讀取函數、優(yōu)化算法函數等。
提供拓展學習資源,如相關書籍、網站和學術論文,鼓勵學員進一步深入學習 Matlab 數學建模。