理論力學(xué)mooc-大連理工大學(xué)

第一部分靜力學(xué)

·引論

剛體靜力學(xué)（statics of rigid bodies）研究剛體（rigid body）在力系的作用下相對于慣性系靜止的力學(xué)規(guī)律。

（1）力學(xué)模型—剛體

在力的作用下不變形的物體稱為剛體。

在實際生活中，完全不變形的物體并不存在，剛體不過是實際物體和構(gòu)件的抽象和簡化。

1靜力學(xué)基礎(chǔ)

1.1力和力矩1.3力偶與力偶矩

1.1.1力的概念1.4物體的受力分析

1.1.2力對點的矩1.4.1約束與約束反力

1.1.3力對軸的矩1.4.2物體的受力分析

1.2力系等效原理

1.2.1力系的主矢和主矩

1.2.2力系等效原理

1.2.3力系等效原理

應(yīng)用于變形體

1靜力學(xué)基礎(chǔ)

1.1力和力矩

1.1.1力的概念

力是物體間的相互作用，作用結(jié)果使物體的運(yùn)動狀態(tài)發(fā)生改變，或使物體產(chǎn)生變形。對剛體而言，力的作用只改變其運(yùn)動狀態(tài)。

·力是矢量

力的三要素（three elements of a force）

兩個共點力的合成又滿足平行四邊形法則，因而力是定位矢量（fixed vector）。

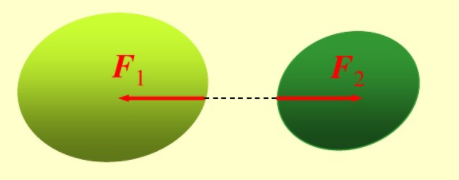
·作用力和反作用力

力的另一重要性質(zhì)是由牛頓第三定律（Newton's third law）所描述的作用力和反作用力之間的關(guān)系，即：

兩個物體之間的作用力與反作用力總是同時存在，且大小相等、方向相反、沿同一直線，并分別作用在兩個不同的物體上。

1.1.2力對點的矩

力矩（moment of a force）是用來量度力使物體產(chǎn)生轉(zhuǎn)動效應(yīng)的概念。·力對點的矩的概念

作用于剛體的力F對空間任意一點O的力矩定義為

式中O點稱為矩心（center of moment），r為矩心O引向力F的作用點A的矢徑，即力對點的矩

（moment of a force about a point）定義為矩心到該力作用點的矢徑與力矢的矢量積。

M。（F）通常被看作為一個定位矢量，習(xí)慣上總是將它的起點畫在矩心O處，但這并不意味著O就是M。（F）的作用點。

力矩矢的三要素

力矩矢的三要素為大小、方向和矩心。

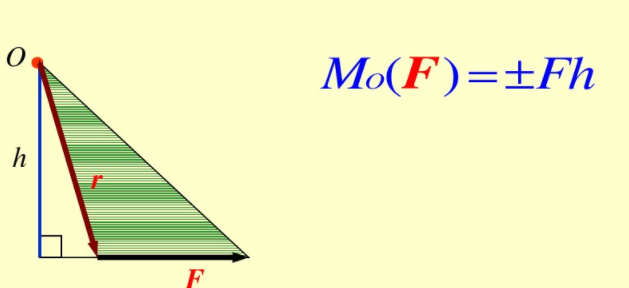
Mo（F）的大小即它的模

式中0為r和F正方向間的夾角，h為矩心到力作用線的垂直距離，常稱為力臂

（moment arm）。M。（F）的方向垂直于r和F所確定的平面，指向由右手定則確定。

平面問題

平面問題中，由于矩心與力矢均在同一個特定的平面內(nèi)，力矩矢總是垂直于該平面，即力矩的方向不變，指向可用正、負(fù)號區(qū)別，故力矩由矢量變成了代數(shù)量，且有

口約束的基本類型

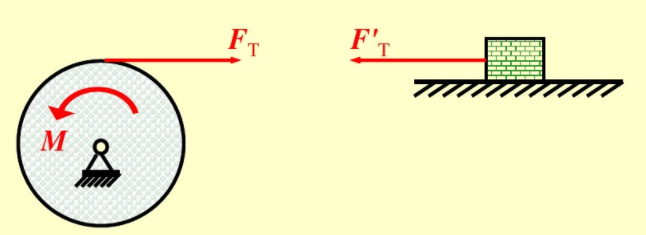
1.柔索

工程中的繩索、鏈條、皮帶等物體可簡化為柔索（flexible cable）。理想化的柔索不可伸長，不計自重，且完全不能抵抗彎曲。

柔索的約束力是沿繩向的拉力。

靜力學(xué)基礎(chǔ)

1.4物體的受力分析（二）

1.4.2物體的受力分析

●選取適當(dāng)?shù)难芯繉ο?/p>

·解除約束●畫受力圖

口分離體和受力圖

被選取作為研究對象，并已解除約束的物體稱為分離體（isolated body）。

當(dāng)研究對象包括幾個物體時，解除約束是指解除周圍物體對它們的全部約束，但不包括這些物體相互之間的聯(lián)系。

畫有分離體及其所受的全部主動力和約束力的圖稱為受力圖（free-body diagram）。

口內(nèi)力和外力

當(dāng)選取由幾個物體所組成的系統(tǒng)作為研究對象時，系統(tǒng)內(nèi)部的物體之間的相互作用力稱為內(nèi)力（internal force），系統(tǒng)之外的物體對系統(tǒng)內(nèi)部的物體的作用力稱為外力（external force）。

顯然，內(nèi)力和外力的區(qū)分是相對的，完全取決于研究對象的選擇。

在作受力圖時不必畫出內(nèi)力。

畫受力圖的步驟如下：

（1）根據(jù)問題的要求選取研究對象，畫出分離體簡圖。

（2）畫出分離體所受的全部主動力，一般不要對已知載荷進(jìn)行靜力等效替換。

（3）在分離體上每一解除約束的地方，根據(jù)約束的類型逐一畫出約束力。

2力系的簡化

尋求一個已知力系的更簡單的等效力系，稱為力系的簡化（reduction of force systems）。

力系的簡化是靜力學(xué)研究的基本問題之一。

本章的主要內(nèi)容包括：匯交力系與力偶系的簡化

空間任意力系的簡化

平行力系的簡化

平行力系中心和重心

2.1匯交力系與力偶系的簡化

2.1.1匯交力系的簡化

各力作用線匯交于一點的力系稱為匯交力系（concurrent force system）。

·匯交力系的簡化一幾何法

匯交力系（F，F(xiàn)…，F(xiàn)。）簡化的結(jié)果為一通過匯交點的合力，合力矢等于原力系的主矢：

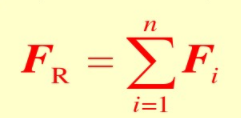
幾何法即是用多邊形法則求這個合力矢。

2.1.2力偶系的簡化

全部由力偶組成的力系稱為力偶系（system of couples）

任意力偶系（M，MMn）的簡化結(jié)果為一合力偶，其合力偶矩等于

3.1力系的平衡方程

3.1.1空間任意力系的平衡方程

3.1.2平面任意力系的平衡方程

3.1.3力系平衡方程的應(yīng)用

3.2物系平衡靜定與超靜定問題

3.2.1物系平衡

3.2.2靜定與超靜定問題

3.2.3物系平衡問題應(yīng)用舉例

3.3考慮摩擦?xí)r的平衡問題

3力系的平衡

3.1力系的平衡方程

3.1.1空間任意力系的平衡方程

空間任意力系平衡的充分必要條件

3.1.3力系平衡方程的應(yīng)用平衡方程主要用于解決以下三方面的問題：

1.求未知約束反力；

2.求平衡位置；

3.確定主動力之間的關(guān)系。

其中重點是問題1。應(yīng)用平衡方程解題的步驟大致如下：

1.選取研究對象，單獨畫出研究對象的受力圖；

2.選取坐標(biāo)系，列平衡方程；

3.解方程（組）；

4.校核及討論。

3.2物系平衡靜定與超靜定問題

3.2.1物系平衡

兩個或兩個以上剛體用一定的方式連接起來組成的系統(tǒng)，稱為剛體系統(tǒng)

（rigid multibody system）。

剛體系統(tǒng)整體處于平衡時，每一局部均處于平衡。

局部：組成系統(tǒng)的單個或幾個剛體所構(gòu)成的子系統(tǒng)。

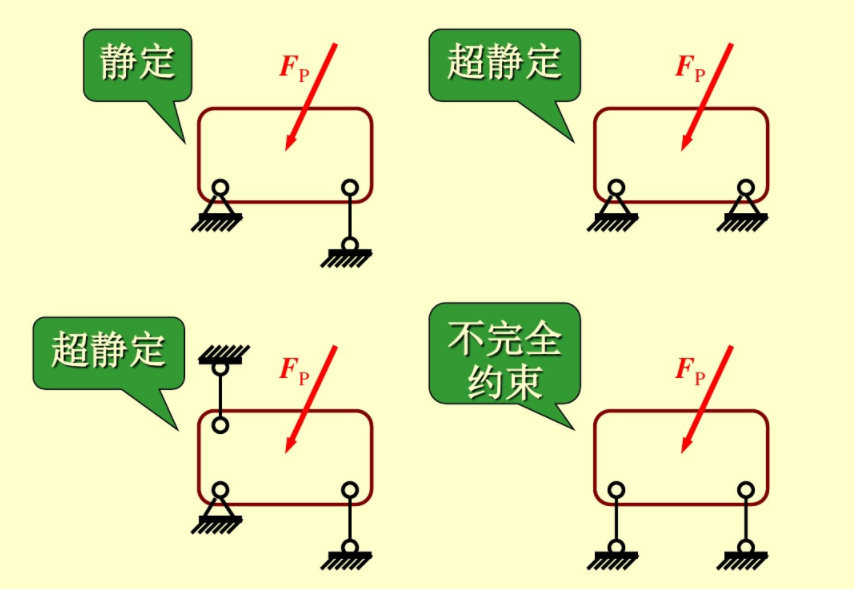
3.2.2靜定與超靜定問題

·靜定間題（statically determinate problems）

來知約束力的數(shù)目=獨立的平衡方程數(shù)

·超靜定間題（statically indeterminate

problems）

未知約束力的數(shù)目>獨立的平衡方程數(shù)

4運(yùn)動學(xué)基礎(chǔ)

4.1點的運(yùn)動學(xué)

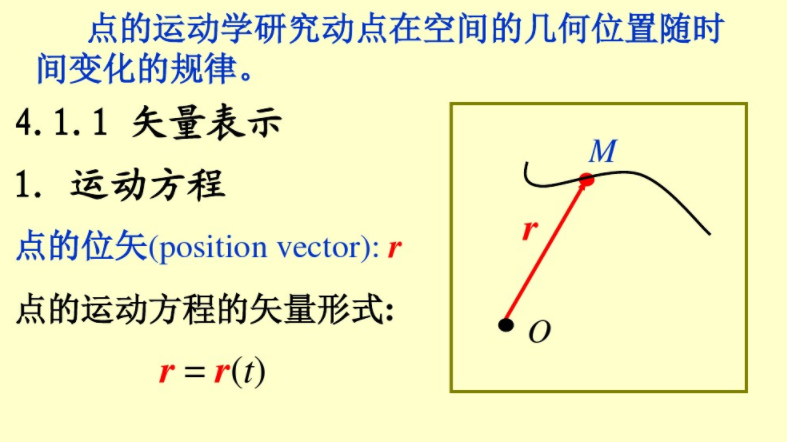
4.1.1矢量表示

4.1.2直角坐標(biāo)法

4.1.3自然法

4.2則體的簡單運(yùn)動

4.2.1則體的平動

4.2.2則體的定軸轉(zhuǎn)動

口剛體的角加速度

定軸轉(zhuǎn)動剛體角速度變化的快慢用角加速度（angular acceleration）來描述，它被定義為角速度對時間的一階導(dǎo)數(shù)，或轉(zhuǎn)角對時間的二階導(dǎo)數(shù)，即

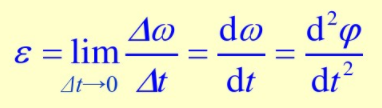
定軸轉(zhuǎn)動剛體的角加速度也是代數(shù)量，正負(fù)號按右手定則確定。s的單位為rad/s2。